BTC_POWER_LA
用戶暫無簡介
BTC_POWER_LA
- 讚賞
- 點讚
- 留言
- 轉發
- 分享
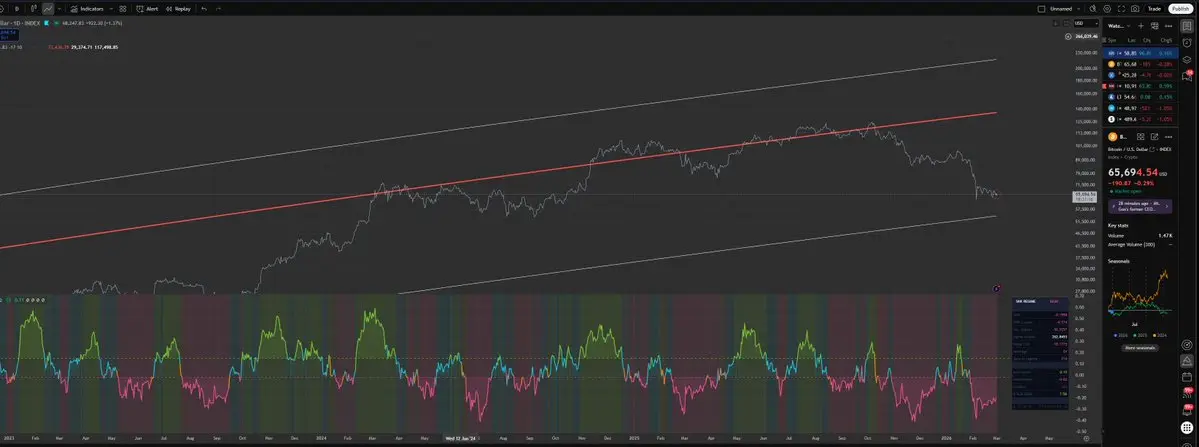
幂律法則有用嗎?
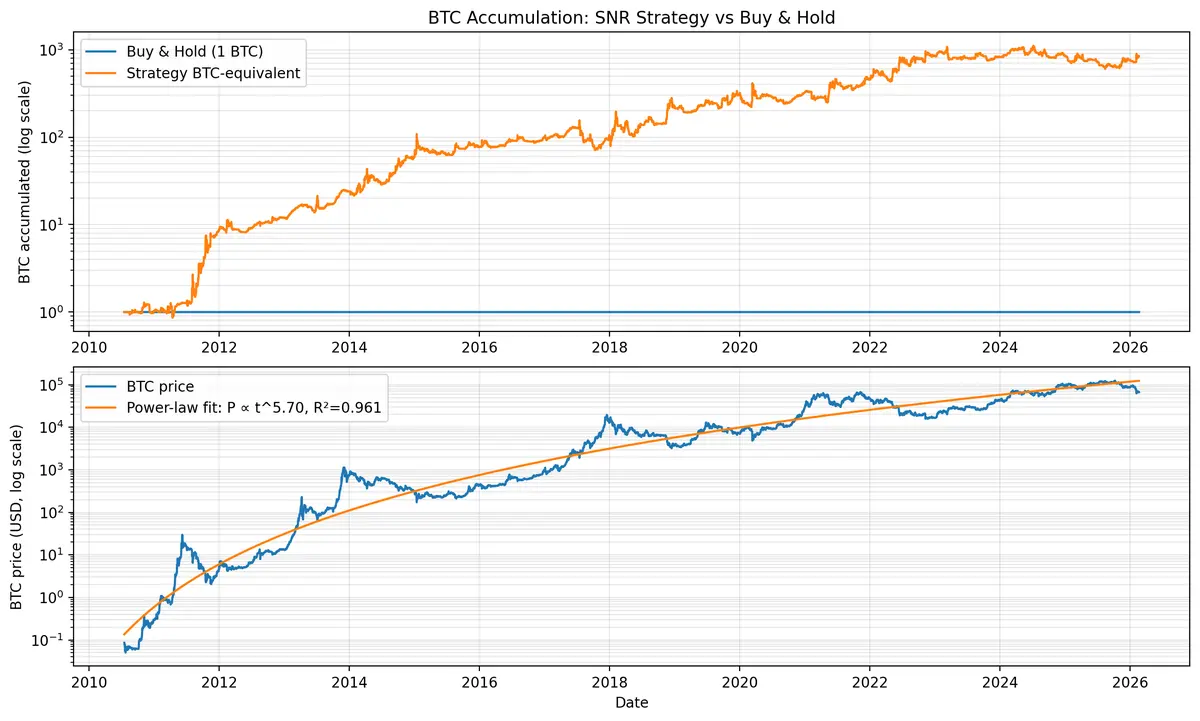
你可以使用一個簡單的策略,結合現貨和永續合約,使用1.5倍槓桿 (且從未被強平),在比特幣的歷史中,讓你從1 BTC賺取800 BTC。
我們早期沒有永續合約,但這展示了可以做到的事情。
你可以使用一個簡單的策略,結合現貨和永續合約,使用1.5倍槓桿 (且從未被強平),在比特幣的歷史中,讓你從1 BTC賺取800 BTC。
我們早期沒有永續合約,但這展示了可以做到的事情。
BTC5.07%
- 讚賞
- 3
- 1
- 轉發
- 分享
cryptos talker  :
:
LFG 🔥這很有趣。如果你以固定間隔進行定期定額(DCA),你的投資仍然會呈現出幾何級數的增長,但斜率會低得多。將幾何級數作為一種信號,可以讓你增加這個斜率。
查看原文- 讚賞
- 1
- 留言
- 轉發
- 分享
你也可以利用冪律來進行智能定投(DCA),以降低回撤並提升整體表現。這種基於冪律的主動定投策略的效果幾乎是傳統方法的10倍。
查看原文- 讚賞
- 點讚
- 留言
- 轉發
- 分享
一個令人毛骨悚然的謀殺之謎。
查看原文
- 讚賞
- 點讚
- 留言
- 轉發
- 分享
- 讚賞
- 1
- 留言
- 轉發
- 分享
我以 Blockstream Capital Partners 顧問的身份參加了一個會議。
查看原文
- 讚賞
- 點讚
- 留言
- 轉發
- 分享
聆聽Zipline這家已在美國運營的無人機配送公司的一場演示。真是令人難以置信。高效、便宜、未來。
查看原文- 讚賞
- 點讚
- 留言
- 轉發
- 分享
目前會議。
查看原文- 讚賞
- 點讚
- 留言
- 轉發
- 分享
我們生活在最好的時代。為什麼人們對一切都感到害怕?
查看原文- 讚賞
- 點讚
- 留言
- 轉發
- 分享
覆蓋看漲期權在熊市期間效果非常好。
查看原文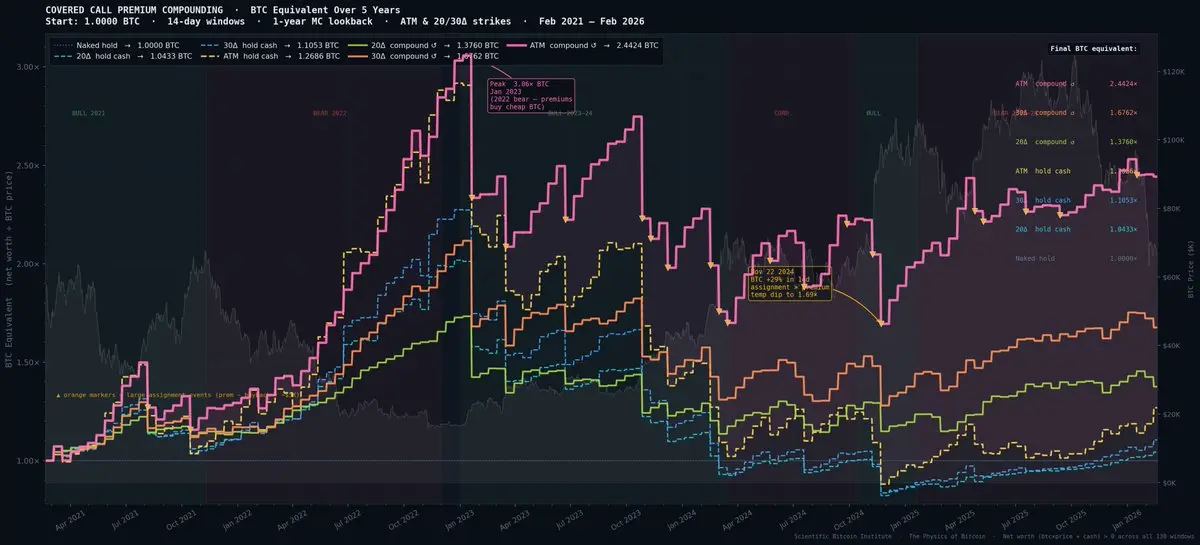
- 讚賞
- 點讚
- 留言
- 轉發
- 分享
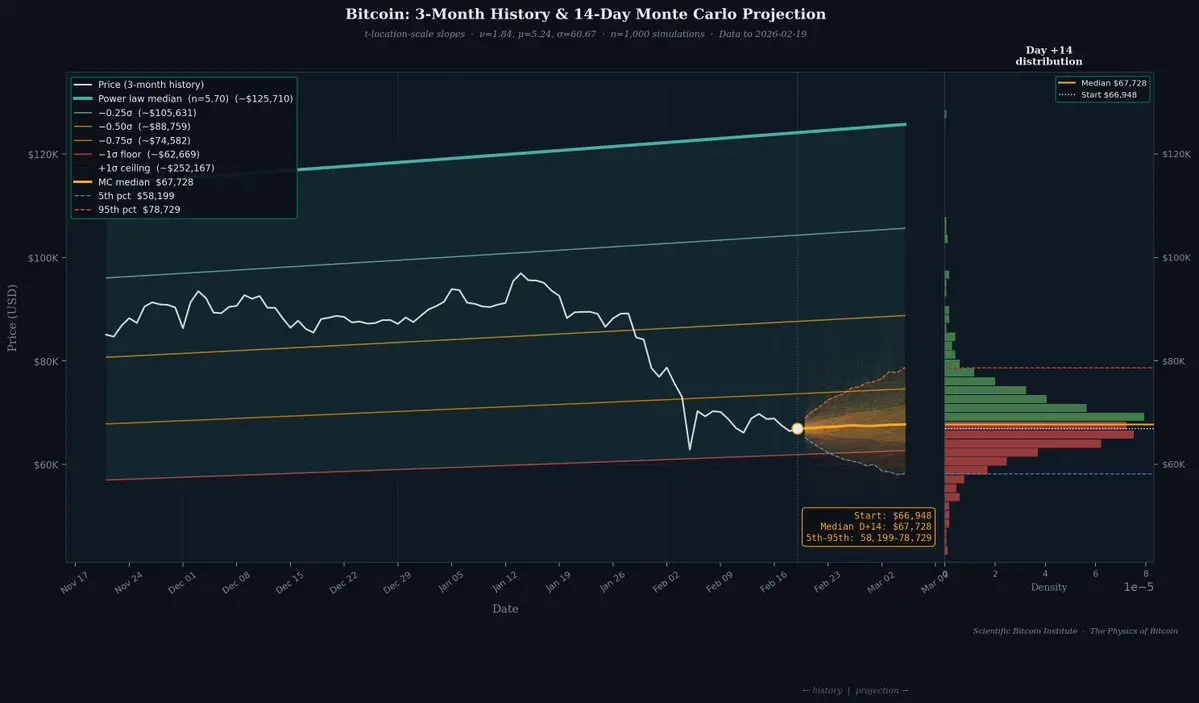
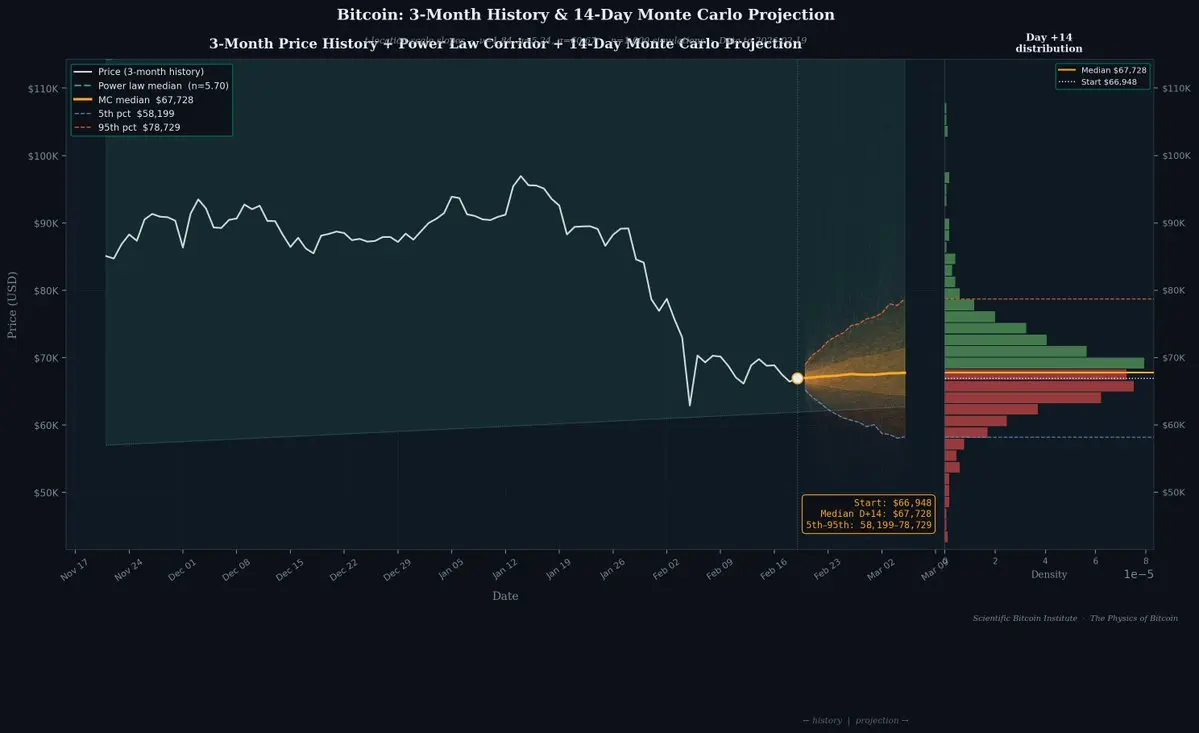
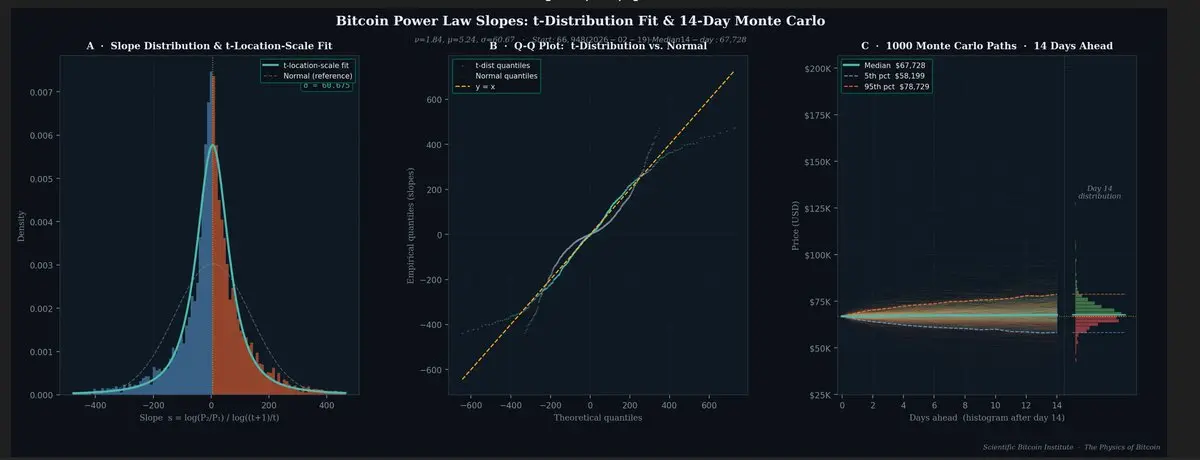
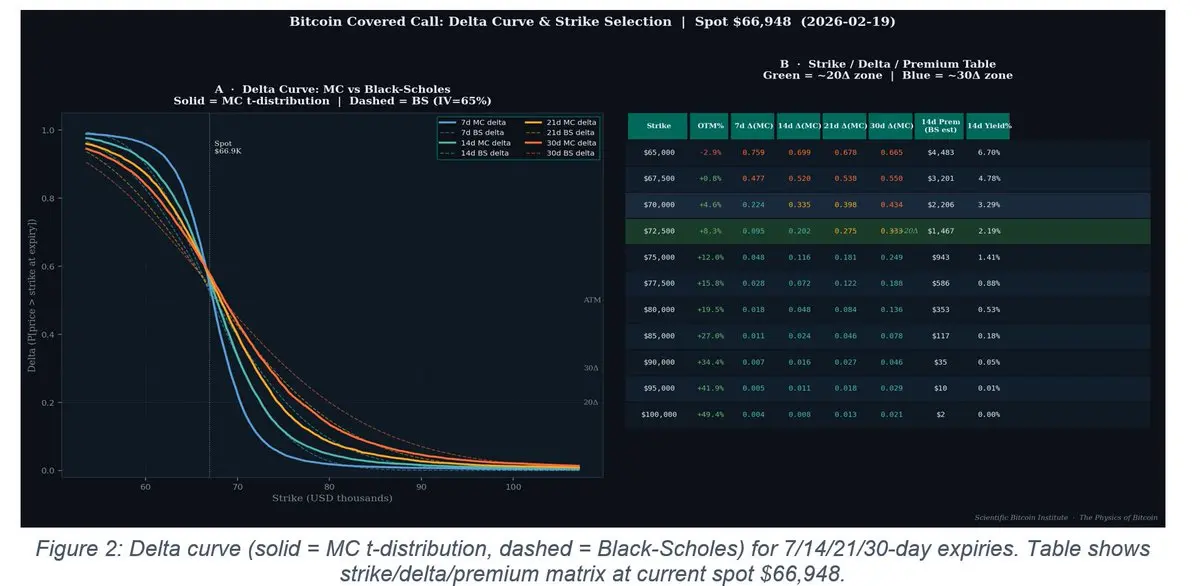
基於冪律斜率的蒙特卡羅模擬比傳統的Black-Scholes (這個萬億美元的方程式)更為保守。
這是因為我們正確考慮了比特幣可能回報分布的尾部較長部分。
這是對比特幣歷史的完整回測。
使用此方法的覆蓋買權可以每月提供非常安全的1%溢價,僅需承擔一點點額外風險即可達到2%。
同時,完全暴露於比特幣的長期增長之中。
這是因為我們正確考慮了比特幣可能回報分布的尾部較長部分。
這是對比特幣歷史的完整回測。
使用此方法的覆蓋買權可以每月提供非常安全的1%溢價,僅需承擔一點點額外風險即可達到2%。
同時,完全暴露於比特幣的長期增長之中。
BTC5.07%
- 讚賞
- 2
- 留言
- 轉發
- 分享
- 讚賞
- 1
- 留言
- 轉發
- 分享
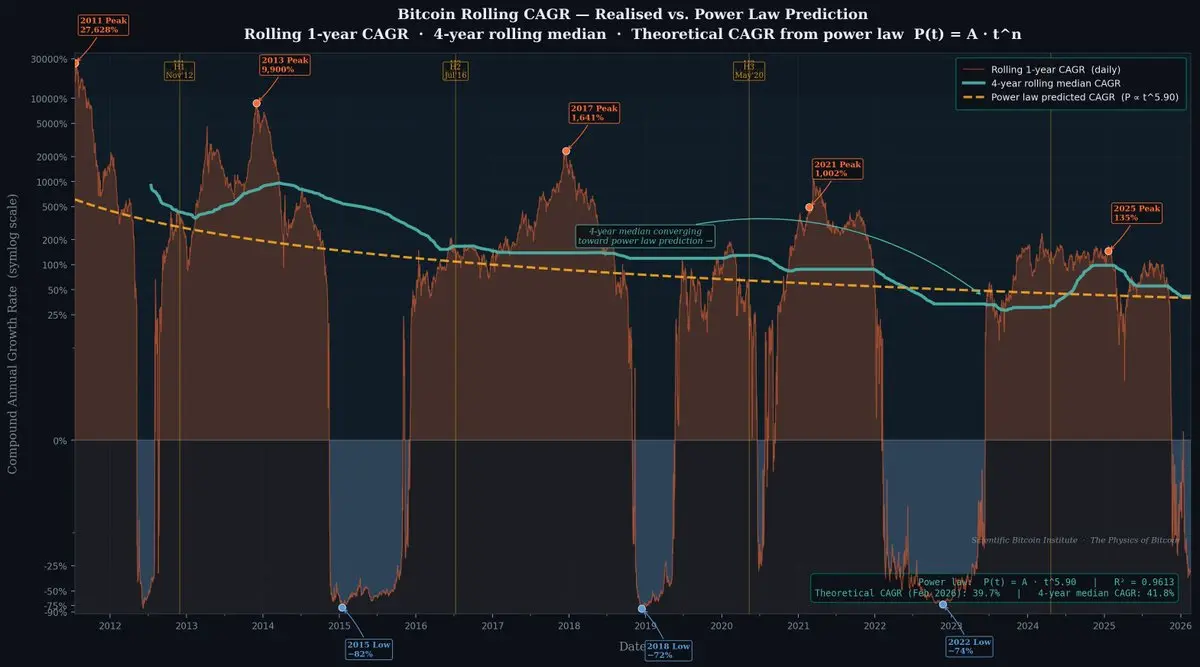
1. 長期收斂 — 金色虛線冪律預測與青色四年中位數自2013年以來穩步收斂,現在基本重疊在約38–42%。這可以說是本書中最具說服力的經驗性驗證:經過平滑的四年回報率正追蹤多年前擬合的數學模型的理論預測。
2. 循環幅度在CAGR(年複合成長率)方面的衰減 — 最高一年的CAGR從2011年的27,628% (降至2013年的9,900% ),再到2017年的1,641% (,2021年的1,002% ),到2025年的135% (。振盪逐漸趨向冪律基線,正如殘差圖以對數單位所顯示。在百分比方面,任何投資者都能感受到這一點。
3. 負CAGR的周期從未持續超過約18個月 — 熊市回撤)−82%、−72%、−74%(明顯位於零線以下,但相較於整個周期來說時間較短。四年中位數從未出現負值。
目前讀數 )2026年2月(:
冪律理論CAGR:39.7%
四年滾動中位數:41.8%
約有2%的差異,這是資料集歷史上最接近的數值
查看原文2. 循環幅度在CAGR(年複合成長率)方面的衰減 — 最高一年的CAGR從2011年的27,628% (降至2013年的9,900% ),再到2017年的1,641% (,2021年的1,002% ),到2025年的135% (。振盪逐漸趨向冪律基線,正如殘差圖以對數單位所顯示。在百分比方面,任何投資者都能感受到這一點。
3. 負CAGR的周期從未持續超過約18個月 — 熊市回撤)−82%、−72%、−74%(明顯位於零線以下,但相較於整個周期來說時間較短。四年中位數從未出現負值。
目前讀數 )2026年2月(:
冪律理論CAGR:39.7%
四年滾動中位數:41.8%
約有2%的差異,這是資料集歷史上最接近的數值
- 讚賞
- 3
- 留言
- 轉發
- 分享
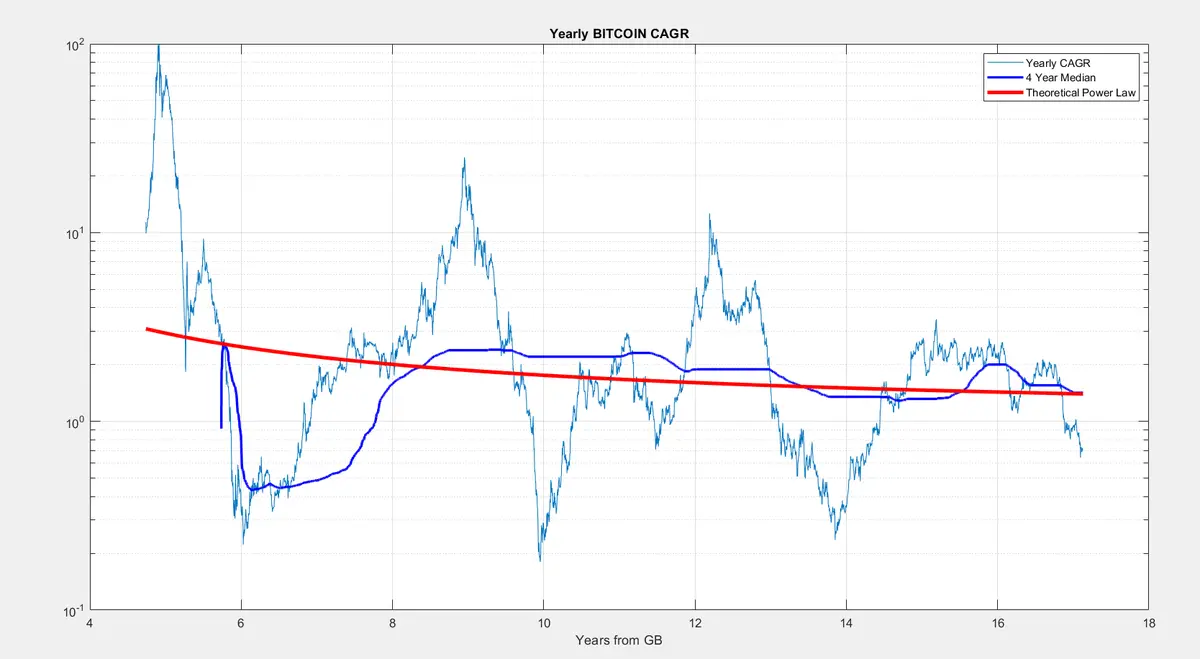
當你長期觀察比特幣的趨勢時,沒有任何改變。即使沒有出現失控的高點,我們的平均回報率也正是由冪律所預測的。目前這些平均的年複合成長率約為40%。再次強調,不要只看某一特定年份,而是要看至少4年的平均值。
BTC5.07%
- 讚賞
- 2
- 留言
- 轉發
- 分享
不。如果我們遵循冪律,年複合成長率(CAGR)在61年後將達到10%。到那時,我們可能已經實現了超比特幣化。
計算方式如下:
公式為 CAGR=( (year+1)/year)^5.9,其中 year 是自創世區塊起的年份。 要知道何時達到10%,我們做:1.1=( (year+1)/year)^5.9,則 1.1^(1/5.9)= year+1/year,解出來為: year= 1/(1.1^(1/5.9)-1)=61.4,也就是2070年。
目前的CAGR平均約為40%。
查看原文計算方式如下:
公式為 CAGR=( (year+1)/year)^5.9,其中 year 是自創世區塊起的年份。 要知道何時達到10%,我們做:1.1=( (year+1)/year)^5.9,則 1.1^(1/5.9)= year+1/year,解出來為: year= 1/(1.1^(1/5.9)-1)=61.4,也就是2070年。
目前的CAGR平均約為40%。
- 讚賞
- 2
- 留言
- 轉發
- 分享
熱門話題
查看更多4247.22萬 熱度
16.01萬 熱度
12.4萬 熱度
167.52萬 熱度
52.08萬 熱度