Memahami Teknologi Linea
Modul ini menampilkan aspek teknis Linea, termasuk kompatibilitasnya dengan Ethereum Virtual Machine (EVM), signifikansi bukti pengetahuan nol, dan implikasi keamanan kriptografi berbasis lattice. Bagian ini bertujuan untuk membekali pembelajar dengan pemahaman yang mendetail tentang teknologi yang membuat Linea menjadi platform blockchain yang aman dan efisien.
Kesesuaian dan Signifikansi Mesin Virtual Ethereum (EVM)

Mesin Virtual Ethereum (EVM) adalah mesin komputasi yang mengeksekusi kontrak pintar di lingkungan blockchain Ethereum. Kompatibilitas Linea dengan EVM melalui Consensys zkEVM memungkinkannya untuk mendukung aplikasi Ethereum yang sudah ada. Kompatibilitas ini memastikan bahwa aplikasi yang dikembangkan untuk Ethereum dapat diterapkan di Linea tanpa perlu rekonfigurasi, sehingga menyederhanakan transisi bagi para pengembang dan menjaga kontinuitas bagi pengguna.
Kompatibilitas EVM meningkatkan kegunaan Linea dengan memungkinkannya mengadopsi kemajuan teknologi dan pembaruan dari jaringan Ethereum. Pengembang mendapat manfaat dari beragam alat dan sumber daya yang telah mapan, memfasilitasi pengembangan dan implementasi aplikasi terdesentralisasi yang lebih mudah. Kompatibilitas ini juga memastikan bahwa Linea dapat memanfaatkan keamanan dan pengujian yang ekstensif yang dilakukan oleh jaringan Ethereum.
Integrasi dengan EVM memposisikan Linea sebagai perpanjangan dari Ethereum, menjadikannya bagian dari ekosistem yang lebih besar daripada platform mandiri. Hubungan ini meningkatkan basis pengguna potensial dan skenario aplikasi untuk Linea, membantu dalam adopsi dan pertumbuhannya dalam komunitas blockchain.
Peran dan Teknologi di Balik Bukti Tanpa Pengetahuan Nol
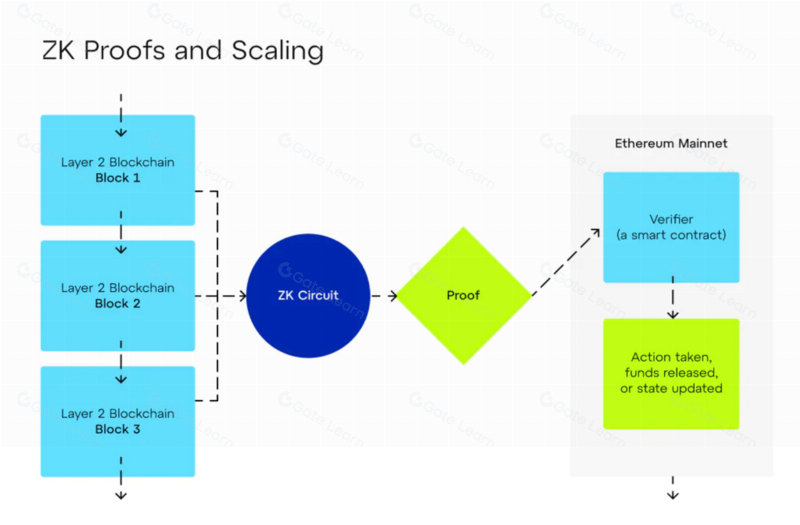
Bukti pengetahuan nol (ZKP) adalah protokol kriptografi yang memungkinkan satu pihak membuktikan kepada pihak lain bahwa suatu pernyataan benar, tanpa mengungkapkan informasi apa pun selain kebenaran pernyataan itu sendiri.
Di Linea, ZKP digunakan untuk meningkatkan privasi dan keamanan transaksi. Mereka memungkinkan validasi transaksi tanpa mengekspos rincian transaksi seperti jumlah, pengirim, atau penerima.
Implementasi ZKP mengurangi jumlah data yang perlu diproses dan disimpan di blockchain, sehingga meningkatkan kecepatan transaksi dan mengurangi biaya. Hal ini sangat penting untuk skalabilitas, karena memungkinkan jaringan Linea untuk menangani volume transaksi yang lebih besar dengan efisien.
ZKP juga berkontribusi terhadap keamanan jaringan Linea dengan meminimalkan paparan data transaksi, yang dapat menjadi target oleh pelaku jahat. Penggunaan ZKP ini membantu dalam menjaga privasi pengguna dan membangun kepercayaan dalam jaringan sebagai platform yang aman untuk melakukan transaksi.
Implikasi Keamanan dari Kriptografi Berbasis Lattice

Kriptografi berbasis kisi membentuk dasar pendekatan kriptografi yang digunakan dalam Linea. Sejauh ini, ini dianggap sangat tahan terhadap serangan komputasi kuantum, menempatkan ekosistem sebagai pilihan yang aman terhadap ancaman potensial yang dapat mengorbankan metode kriptografi lainnya.
Kriptografi berbasis kisi melibatkan pembangunan kisi matematika kompleks yang sulit dipecahkan tanpa kunci yang benar.
Jenis kriptografi ini digunakan dalam Linea untuk mengamankan transaksi dan untuk menghasilkan bukti tanpa pengetahuan. Kekuatan kriptografi berbasis kisi terletak pada kompleksitas dan ketahanannya terhadap teknik dekripsi konvensional, menjadikannya pilihan yang kuat untuk mengamankan jaringan blockchain.
Penggunaan kriptografi berbasis jala tidak hanya meningkatkan fitur keamanan Linea tetapi juga memastikan keberlanjutan jangka panjang dan keandalan jaringan, bahkan ketika kemajuan dalam teknologi komputasi terus berkembang.
Sorotan
- Linea kompatibel dengan Mesin Virtual Ethereum (EVM), memungkinkan aplikasi Ethereum yang ada berjalan secara efisien di jaringannya.
- Kompatibilitas EVM memudahkan penggunaan alat pengembangan yang sudah mapan dan sumber daya, menyederhanakan proses implementasi bagi pengembang dan meningkatkan kegunaan platform.
- Bukti pengetahuan nol (ZKP) di Linea memastikan privasi transaksi melalui validasi tanpa mengungkap rincian transaksi, meningkatkan keamanan dan skalabilitas.
- Implementasi ZKP mengurangi kemacetan blockchain dengan meminimalkan data yang diproses dan disimpan, sehingga mempercepat kecepatan transaksi dan menurunkan biaya.
- Kriptografi berbasis kisi mengamankan jaringan Linea dari ancaman komputasi kuantum potensial dan memberikan dasar yang kuat untuk menjaga integritas data dan privasi pengguna.





